Java版-数据结构-队列（循环队列）

原创
顾立剑
数据结构
0 ℃

前情回顾

在上一篇，笔者给大家介绍了数组队列，并且在文末提出了数组队列实现上的劣势，以及带来的性能问题（因为数组队列，在出队的时候，我们往往要将数组中的元素往前挪动一个位置，这个动作的时间复杂度O(n)级别），如果不清楚的小伙伴欢迎查看阅读。为了方便大家查阅，笔者在这里贴出相关的地址：

为了解决数组队列带来的问题，本篇给大家介绍一下循环队列。

思路分析图解

啰嗦一下，由于笔者不太会弄贴出来的图片带有动画效果，比如元素的移动或者删除（毕竟这样看大家比较直观），笔者在这里只能通过静态图片的方式，帮助大家理解实现原理，希望大家不要见怪，如果有朋友知道如何搞的话，欢迎在评论区慧言。

在这里，我们声明了一个容量大小为8的数组，并标出了索引0-7，然后使用front和tail分别来表示队列的，队首和队尾；在下图中，front和tail的位置一开始都指向是了索引0的位置，这意味着当front == tai的时候 队列为空 大家务必牢记这一点，以便区分后面介绍队列快满时的临界条件

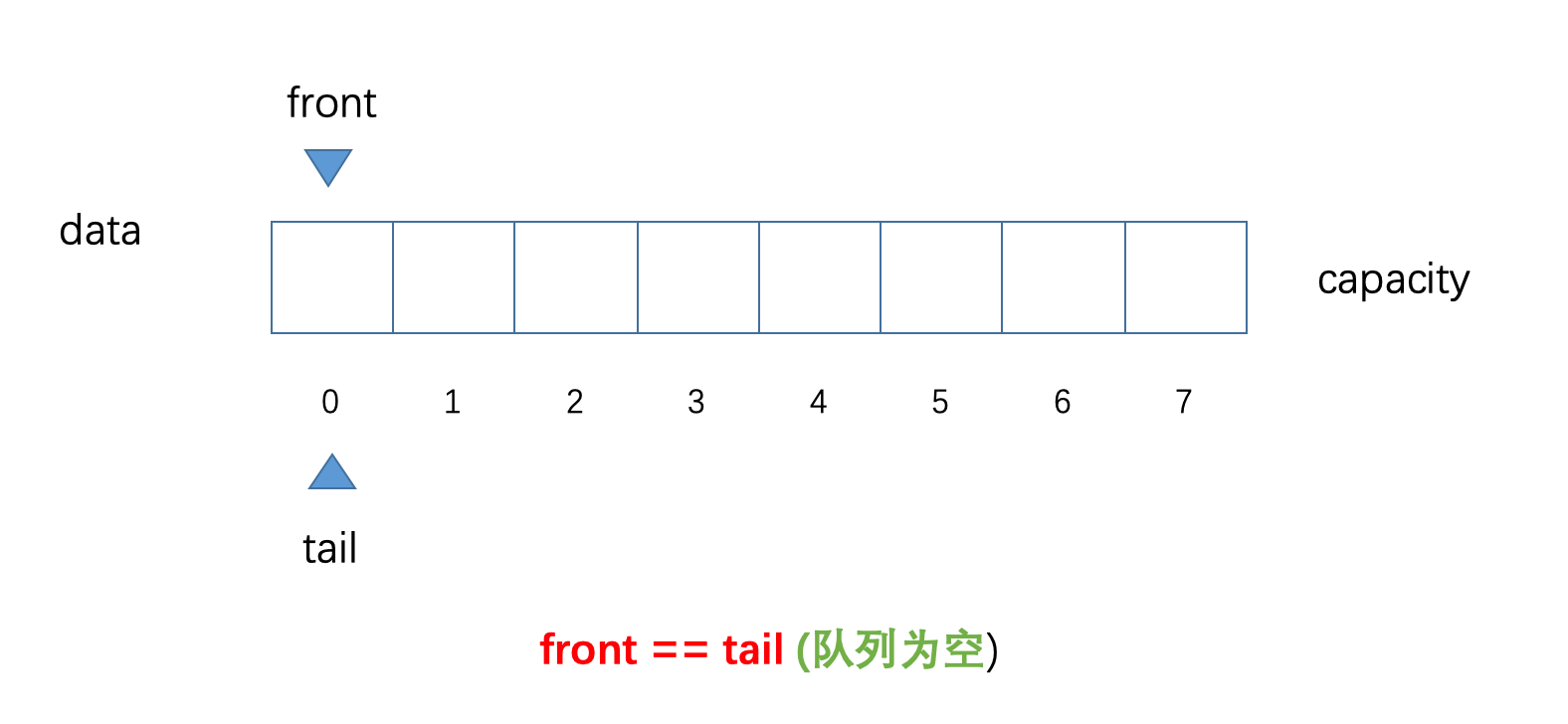
image-20190321003646859

为了大家更好地理解下面的内容，在这里，我简单做几点说明

  • front：表示队列队首，始终指向队列中的第一个元素（当队列空时，front指向索引为0的位置）

  • tail：表示队列队尾，始终指向队列中的最后一个元素的下一个位置

  • 元素入队，维护tail的位置，进行tail++操作

  • 元素出队，维护front的位置，进行front++操作

    上面所说的，元素进行入队和出队操作，都简单的进行++操作，来维护tail和front的位置，其实是不严谨的，正确的维护tail的位置应该是(tail + 1) % capacity，同理front的位置应该是(front + 1) % capacity，这也是为什么叫做循环队列的原因，大家先在这里知道下，暂时不理解也没关系，后面相信大家会知晓。

    下面我们看一下，现在如果有一个元素a入队，现在的示意图：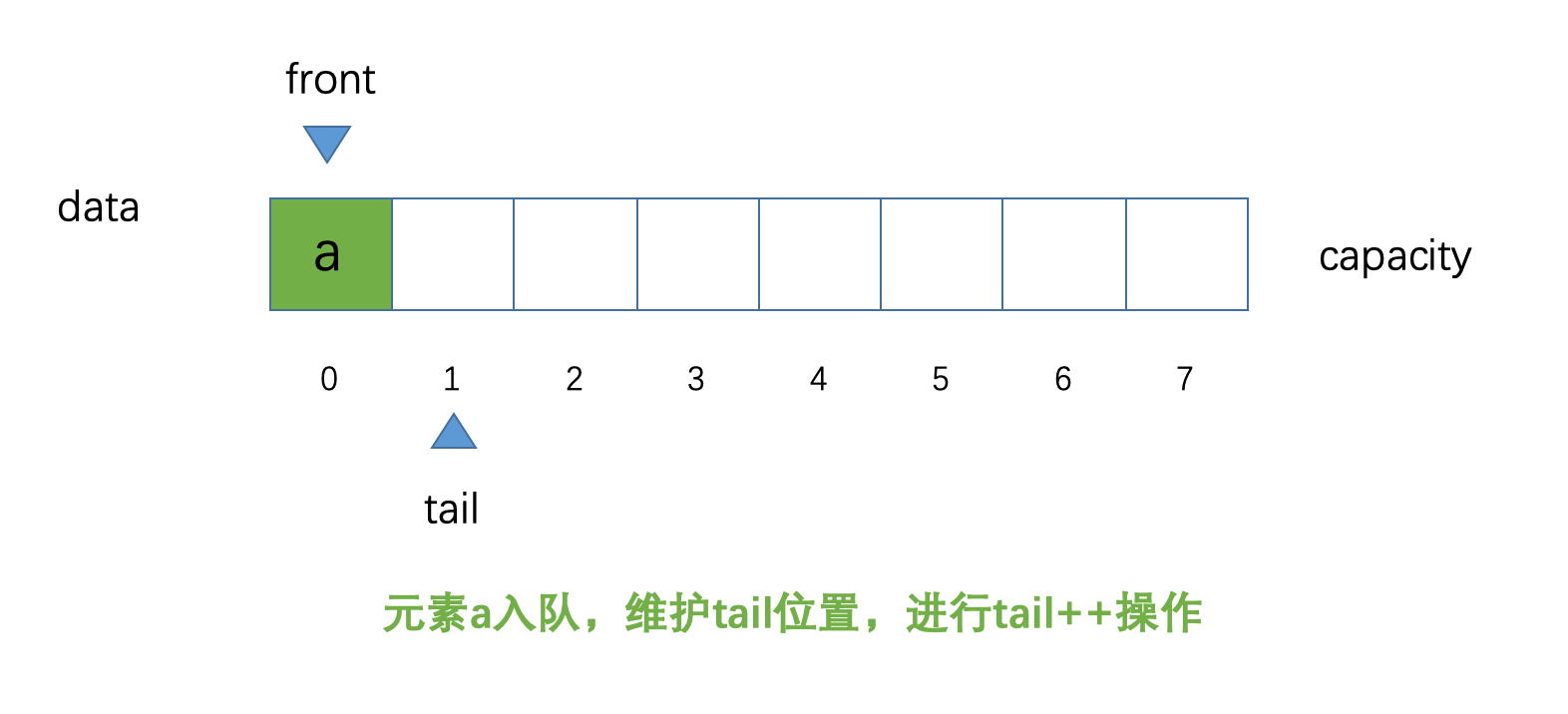

    image-20190321011926946

    我们现在看到了元素a入队，我们的tail指向的位置发生了变化，进行了++操作，而front的位置，没有发生改变，仍旧指向索引为0的位置，还记得笔者上面所说的，front的位置，始终指向队列中的第一个元素，tail的位置，始终指向队列中的最后一个元素的下一个位置

    现在，我们再来几个元素b、c、d、e进行入队操作，看一下此时的示意图：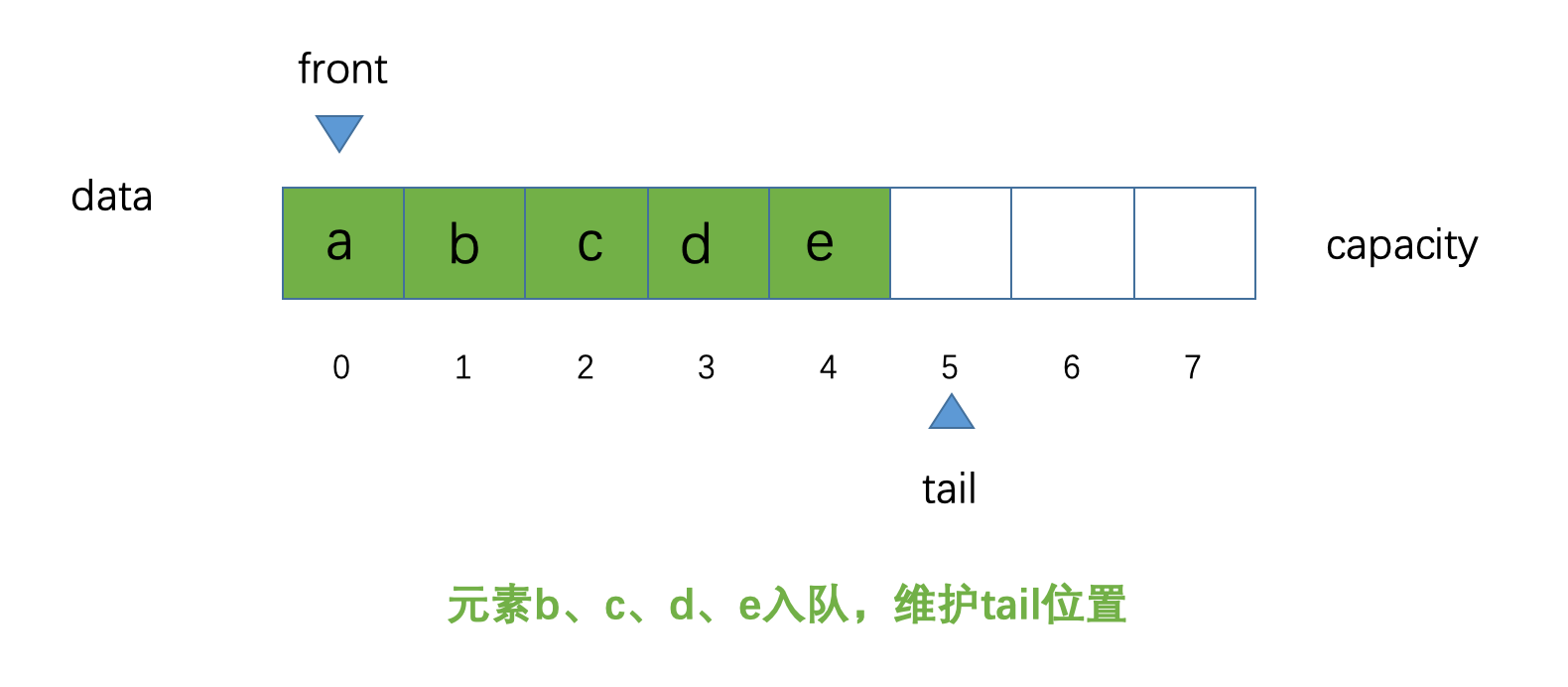

    image-20190321012501661

    想必大家都能知晓示意图是这样，好像没什么太多的变化（还请大家别着急，笔者这也是方便大家理解到底是什么循环队列，还请大家原谅我O(∩_∩)O哈！）

    看完了元素的入队的操作情况，那现在我们看一下，元素的出队操作是什么样的？

    元素a出队，示意图如下：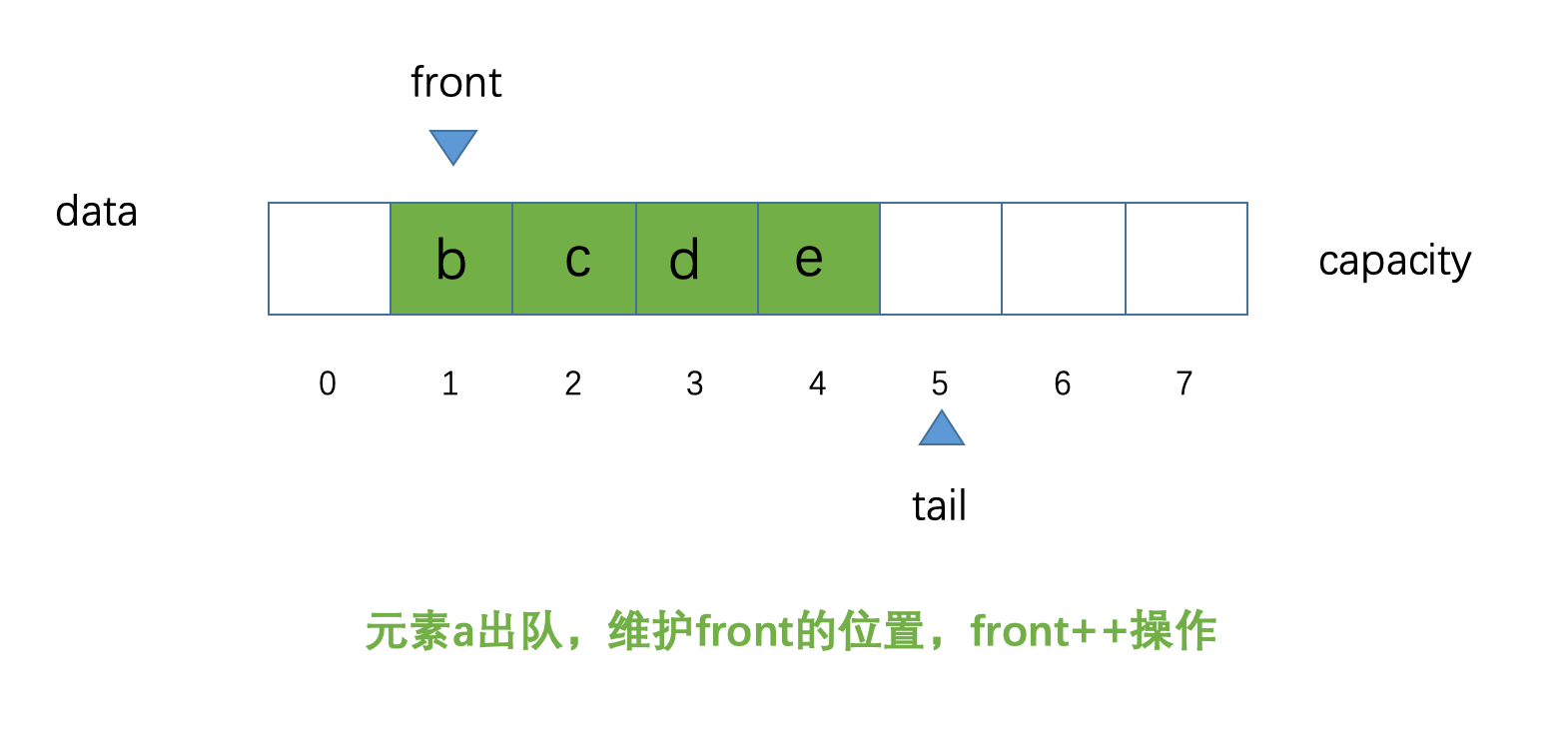

    image-20190321012912749

    现在元素a已经出队，front的位置指向了索引为1的位置，现在数组中所有的元素不再需要往前挪动一个位置

    这一点和我们的数组队列（我们的数组队列需要元素出队，后面的元素都要往前挪动一个位置）完全不同，我们只需要改变一下front的指向就可以了，由之前的O(n)操作，变成了O(1)的操作

    我们再次进行元素b出队，示意图如下：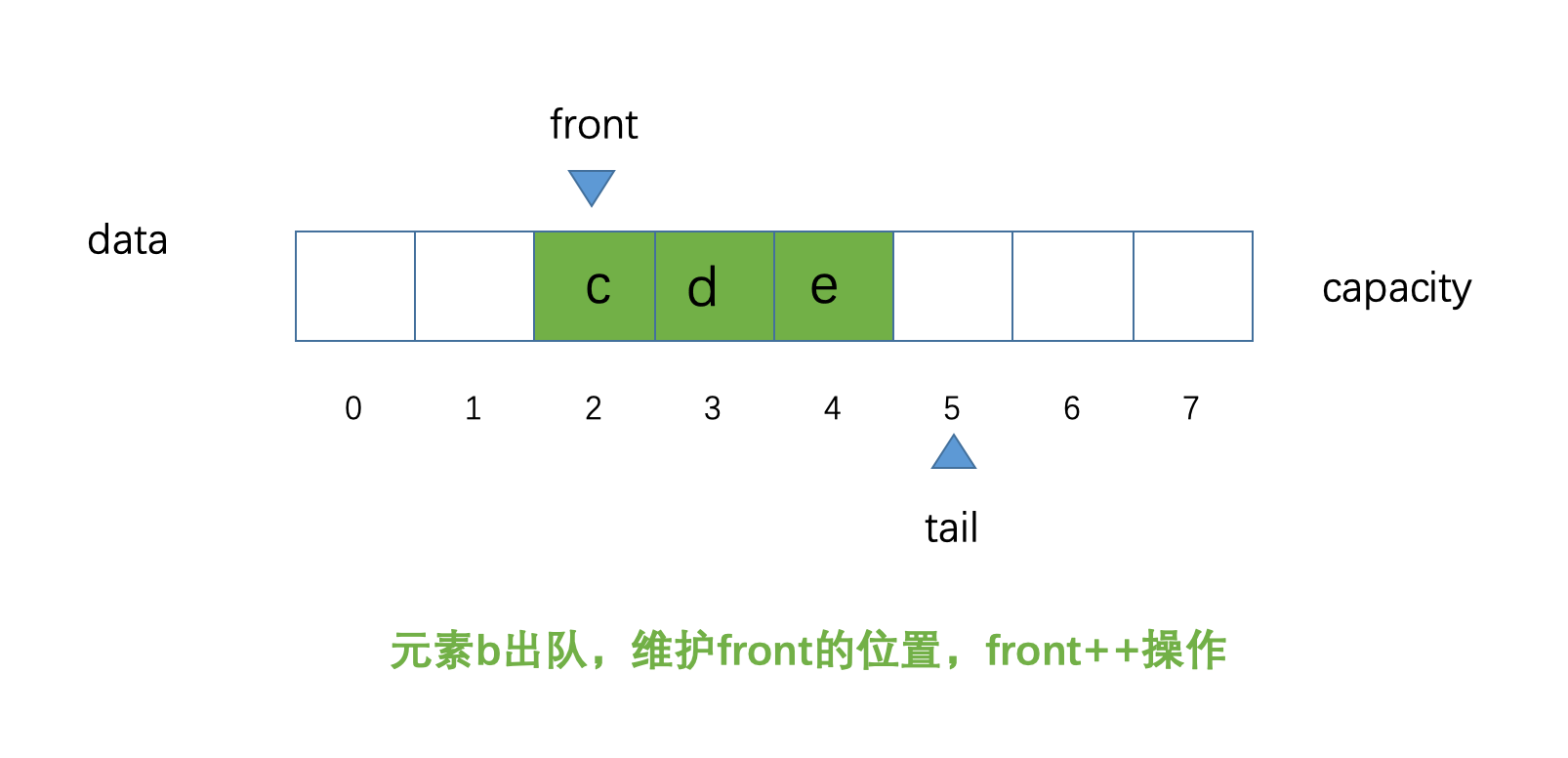

    image-20190321014047456

    到这里，可能有的小伙伴会问，为什么叫做，循环队列？那么现在我们尝试一下，我们让元素f、g分别进行入队操作，此时的示意图如下：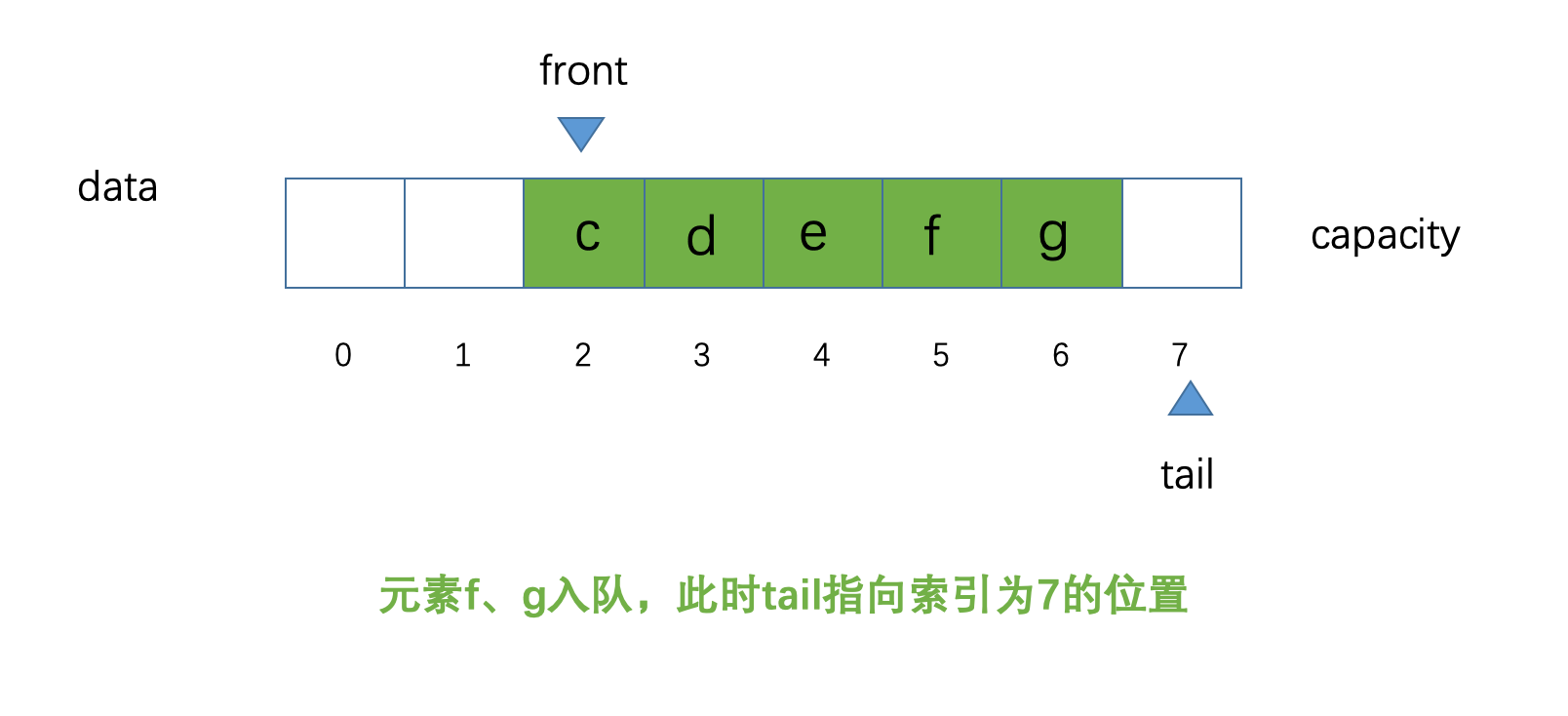

    image-20190321015054219

    大家目测看下来还是没什么变化，如果此时，我们再让一个元素h元素进行入队操作，那么问题来了我们的tail的位置该如何指向呢？示意图如下：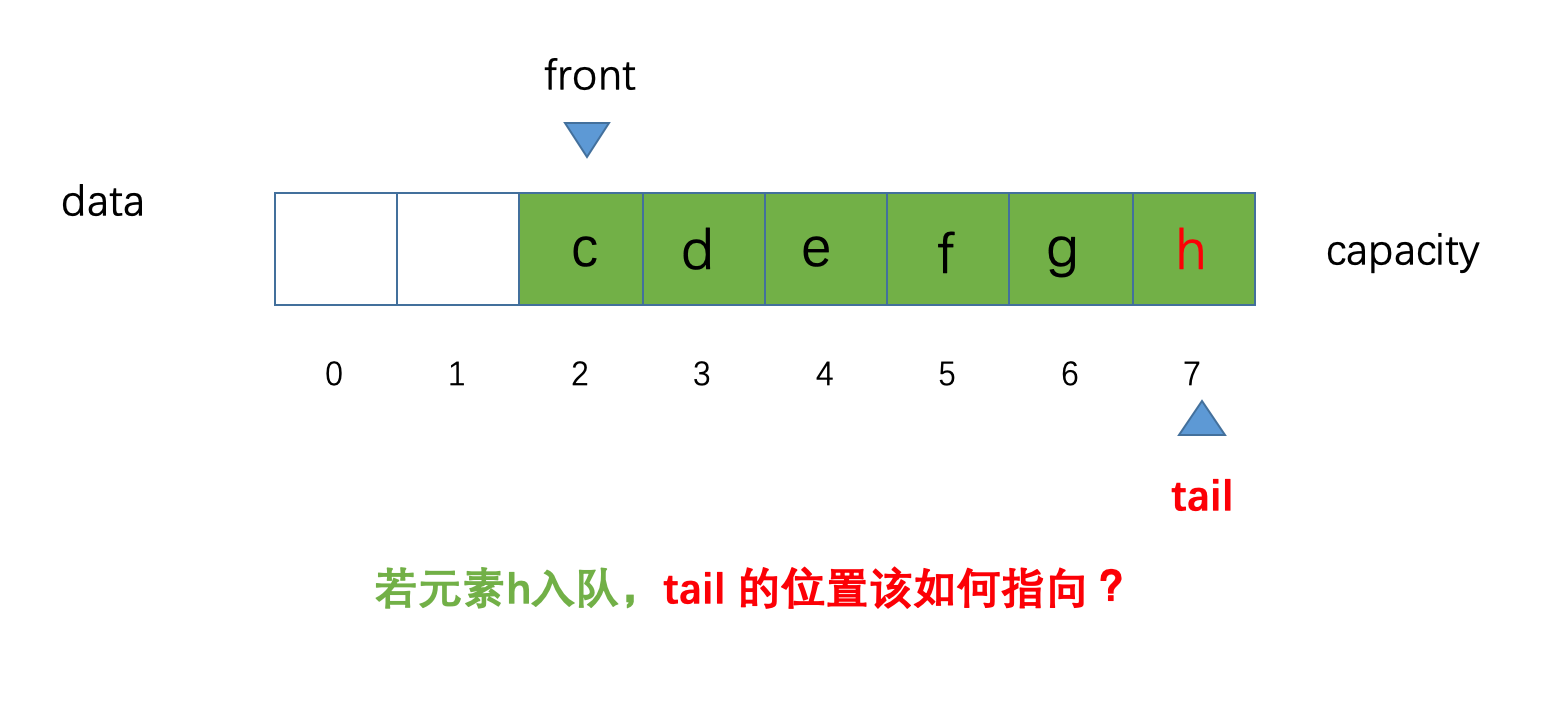

    image-20190321020004501根据我们之前说的，元素入队：维护tail的位置，进行tail++操作，而此时我们的tail已经指向了索引为7的位置，如果我们此时对tail进行++操作，显然不可能（数组越界）

    细心的小伙伴，会发现此时我们的队列并没有满，还剩两个位置（这是因为我们元素出队后，当前的空间，没有被后面的元素挤掉），大家可以把我们的数组想象成一个环状，那么索引7之后的位置就是索引0

    如何才能从索引7的位置计算到索引0的位置，之前我们一直说进行tail++操作，笔者也在开头指出了，这是不严谨的，应该的是(tail + 1) % capacity这样就变成了(7 + 1) % 8等于 0

    所以此时如果让元素h入队，那么我们的tail就指向了索引为0的位置，示意图如下：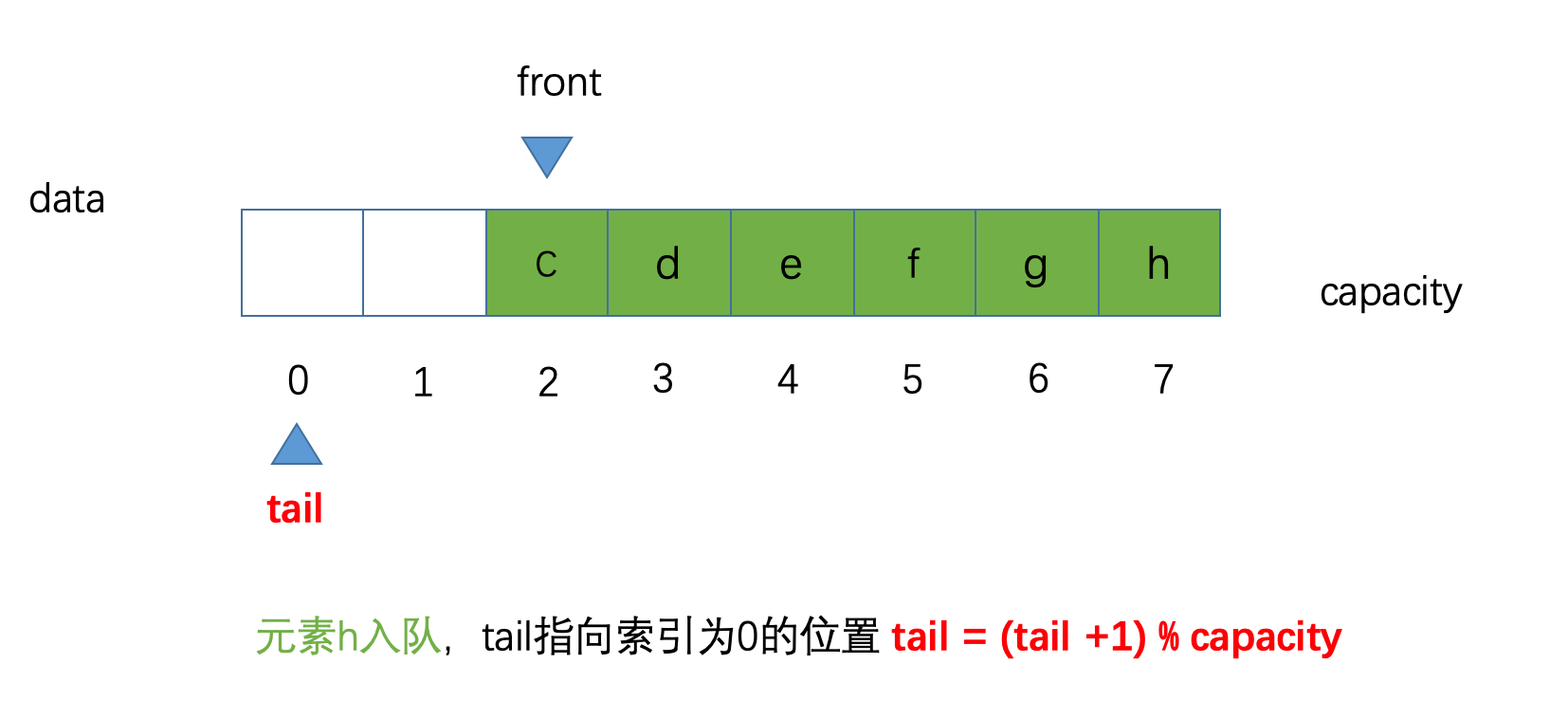

    image-20190323120553239

    假设现在又有新的元素k入队了，那么tail的位置等于（tail + 1） % capacity 也就是（0 + 1）% 8等于1就指向了索引为1的位置

    image-20190323123428055

    那么问题来了，我们的循环队列还能不能在进行元素入队呢？我们来分析一下，从图中显示，我们还有一个索引为0的空的空间位置，也就是此时tail指向的位置

    按照之前的逻辑，假设现在能放入一个新元素，我们的tail进行(tail +1) % capacity计算结果为2（如果元素成功入队，此时队列已经满了），此时我们会发现表示队首的front也指向了索引为2的位置

    如果新元素成功入队的话，我们的tail也等于2，那么此时就成了 tail == front ，一开始我们提到过，当队列为空的tail == front，现在呢，如果队列为满时tail也等于front，那么我们就无法区分，队列为满时和队列为空时收的情况了

    所以，在循环队列中，我们总是浪费一个空间，来区分队列为满时和队列为空时的情况，也就是当 ( tail + 1 ) % capacity == front的时候，表示队列已经满了，当front == tail的时候，表示队列为空。

    image-20190323124927705

    了解了循环队列的实现原理之后，下面我们用代码实现一下。

代码实现

接口定义 ：Queue

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
public interface Queue<E> {
    /**
     * 入队
     *
     * @param e
     */
    void enqueue(E e);

    /**
     * 出队
     *
     * @return
     */
    E dequeue();

    /**
     * 获取队首元素
     *
     * @return
     */
    E getFront();

    /**
     * 获取队列中元素的个数
     *
     * @return
     */
    int getSize();

    /**
     * 判断队列是否为空
     *
     * @return
     */
    boolean isEmpty();
}

接口实现：LoopQueue

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
public class LoopQueue<E> implements Queue<E> {
    /**
     * 承载队列元素的数组
     */
    private E[] data;
    /**
     * 队首的位置
     */
    private int front;
    /**
     * 队尾的位置
     */
    private int tail;
    /**
     * 队列中元素的个数
     */
    private int size;

    /**
     * 指定容量，初始化队列大小
     * (由于循环队列需要浪费一个空间，所以我们初始化队列的时候，要将用户传入的容量加1)
     *
     * @param capacity
     */
    public LoopQueue(int capacity) {
        data = (E[]) new Object[capacity + 1];
    }

    /**
     * 模式容量，初始化队列大小
     */
    public LoopQueue() {
        this(10);
    }


    @Override
    public void enqueue(E e) {
        // 检查队列为满
        if ((tail + 1) % data.length == front) {
            // 队列扩容
            resize(getCapacity() * 2);
        }
        data[tail] = e;
        tail = (tail + 1) % data.length;
        size++;
    }


    @Override
    public E dequeue() {
        if (isEmpty()) {
            throw new IllegalArgumentException("队列为空");
        }
        // 出队元素
        E element = data[front];
        // 元素出队后，将空间置为null
        data[front] = null;
        // 维护front的索引位置(循环队列)
        front = (front + 1) % data.length;
        // 维护size大小
        size--;

        // 元素出队后，可以指定条件，进行缩容
        if (size == getCapacity() / 2 && getCapacity() / 2 != 0) {
            resize(getCapacity() / 2);
        }
        return element;
    }

    @Override
    public E getFront() {
        if (isEmpty()) {
            throw new IllegalArgumentException("队列为空");
        }
        return data[front];
    }

    @Override
    public int getSize() {
        return size;
    }

    @Override
    public boolean isEmpty() {
        return front == tail;
    }


    // 队列快满时，队列扩容；元素出队操作，指定条件可以进行缩容
    private void resize(int newCapacity) {
        // 这里的加1还是因为循环队列我们在实际使用的过程中要浪费一个空间
        E[] newData = (E[]) new Object[newCapacity + 1];
        for (int i = 0; i < size; i++) {
            // 注意这里的写法：因为在数组中，front 可能不是在索引为0的位置，相对于i有一个偏移量
            newData[i] = data[(i + front) % data.length];
        }
        // 将新的数组引用赋予原数组的指向
        data = newData;
        // 充值front的位置（front总是指向队列中第一个元素）
        front = 0;
        // size 的大小不变，因为在这过程中，没有元素入队和出队
        tail = size;
    }


    private int getCapacity() {
        // 注意：在初始化队列的时候，我们有意识的为队列加了一个空间，那么它的实际容量自然要减1
        return data.length - 1;
    }

    @Override
    public String toString() {
        return "LoopQueue{" +
                "【队首】data=" + Arrays.toString(data) + "【队尾】" +
                ", front=" + front +
                ", tail=" + tail +
                ", size=" + size +
                ", capacity=" + getCapacity() +
                '}';
    }
}

测试类：LoopQueueTest

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public class LoopQueueTest {
    @Test
    public void testLoopQueue() {
        LoopQueue<Integer> loopQueue = new LoopQueue<>();
        for (int i = 0; i < 10; i++) {
            loopQueue.enqueue(i);
        }
        // 初始化队列数据
        System.out.println("原始队列: " + loopQueue);
        // 元素0出队
        loopQueue.dequeue();
        System.out.println("元素0出队: " + loopQueue);
        loopQueue.dequeue();
        System.out.println("元素1出队: " + loopQueue);
        loopQueue.dequeue();
        System.out.println("元素2出队: " + loopQueue);
        loopQueue.dequeue();
        System.out.println("元素3出队: " + loopQueue);
        loopQueue.dequeue();
        System.out.println("元素4出队,发生缩容: " + loopQueue);
        // 队首元素
        System.out.println("队首元素：" + loopQueue.getFront());
    }
}
测试结果：
1
2
3
4
5
6
7
原始队列: LoopQueue{【队首】data=[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, null]【队尾】, front=0, tail=10, size=10, capacity=10}
元素0出队: LoopQueue{【队首】data=[null, 1, 2, 3, 4, 5, 6, 7, 8, 9, null]【队尾】, front=1, tail=10, size=9, capacity=10}
元素1出队: LoopQueue{【队首】data=[null, null, 2, 3, 4, 5, 6, 7, 8, 9, null]【队尾】, front=2, tail=10, size=8, capacity=10}
元素2出队: LoopQueue{【队首】data=[null, null, null, 3, 4, 5, 6, 7, 8, 9, null]【队尾】, front=3, tail=10, size=7, capacity=10}
元素3出队: LoopQueue{【队首】data=[null, null, null, null, 4, 5, 6, 7, 8, 9, null]【队尾】, front=4, tail=10, size=6, capacity=10}
元素4出队,发生缩容: LoopQueue{【队首】data=[5, 6, 7, 8, 9, null]【队尾】, front=0, tail=5, size=5, capacity=5}
队首元素：5

完整版代码GitHub仓库地址：Java版数据结构-队列（循环队列） 欢迎大家【关注】和【Star】

至此笔者已经为大家带来了数据结构：静态数组、动态数组、栈、数组队列、循环队列；接下来，笔者还会一一的实现其它常见的数组结构，大家一起加油。

  • 静态数组
  • 动态数组
  • 栈
  • 数组队列
  • 循环队列
  • 链表
  • 循环链表
  • 二分搜索树
  • 优先队列
  • 堆
  • 线段树
  • 字典树
  • AVL
  • 红黑树
  • 哈希表

  • ….

    持续更新中，欢迎大家关注公众号：小白程序之路（whiteontheroad），第一时间获取最新信息！！！

    小白程序之路

数据结构